Алгоритмы обработки данных
Коднянко В.А.
Лабораторный
практикум
Тема № 2
Циклические алгоритмы
Основной частью циклического алгоритма является цикл - многократно повторяемая последовательность
исполняемых инструкций. Циклы делятся на две группы. К первой группе
относятся циклы с наперед известным числом повтором. Ко второй группе
относятся циклы, которые выполняются до тех пор, пока не выполнится
определенное логическое условие, то есть число повторов такого цикла наперед
неизвестно.
2.1. Цикл с неизвестным числом
повторов
Примером такого цикла может
служить алгоритмическое решение задачи о нахождении
корня нелинейного уравнения.
Нелинейным
называется всякое уравнение f(x) = 0, которое нельзя
представить в виде линейного уравнения a•x + b = 0.
Если нелинейное уравнение достаточно сложно, то его обычно не удается решить
аналитическими методами. В таких случаях его корни отыскивают приближенно с
использованием какого-либо вычислительного метода. Существует несколько
методов, которые находят применение при решении этого класса задач. К их
числу относятся метод итерации, метод хорд, метод Ньютона (метод
касательных), метод бисекции (метод половинного деления) и их комбинации.
Однако
большинство этих методов не гарантируют достижение результата, т. к.
развитие вычислительного процесса в значительной мере зависит от поведения
функции f(x) и нередко именно это обстоятельство делает такой метод
нерезультативным. В особенности это относится к различным вариантам метода
Ньютона и методу итераций.
Среди методов
решения нелинейных уравнений следует выделить метод бисекции и метод хорд,
которые лишены этих недостатков.
Рассмотрим один из них – метод бисекции. Если функция f(x)
непрерывна и известно, что на концах какого-либо отрезка [a, b] она
имеет противоположные по знаку значения (f(a)•f(b)<0), то метод
гарантирует нахождение одного корня на этом отрезке. Для большинства
практических задач такие условия вполне приемлемы, а из практических
соображений путем несложных рассуждений или вычислений обычно без особых
трудностей удается отделить отрезок, на котором находится подлежащий
определению корень x0.
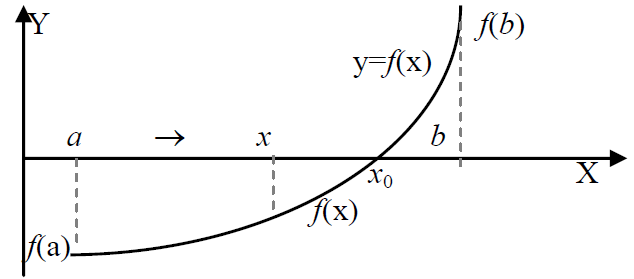
Рис. 1. К методу бисекции
Суть метода
проста. Пусть дан отрезок [a, b] и f(a) < 0, f(b) > 0.
Поскольку функция непрерывна и на концах отрезка [a, b] имеет
противоположные знаки, то где-то во внутренней точке x0
отрезка она пересечет ось абсцисс. Эта точка является искомым корнем.
Вычислим значение функции в середине отрезка x = (a+b)/2. Если f(x)=0,
то корень найден. Если это значение окажется отрицательным, то отбросим
левую часть отрезка, оставив для дальнейшего поиска отрезок [x, b],
для которого выполняются те же условия f(x)<0, f(b)>0. Если значение
положительно, оставим отрезок [a, x], для которого f(a)<0, f(x)>0.
При любом из двух вариантов область поиска корня уменьшится вдвое
и в точку x переносится либо
a либо b.
К оставшемуся отрезку применим тот же метод. Будем продолжать процесс
деления отрезков до тех пор, пока длина последнего отрезка не станет меньше
какого-либо малого числа e. Корнем можно
считать любой конец этого отрезка или их среднее арифметическое, что
предпочтительнее. Для случая f(a)>0, f(b)<0 рассуждения аналогичны.
Построим алгоритм
нахождения корня нелинейного уравнения g(x)= 5х4 – 20х3
– 16х +1 с точностью e = 0,001.
График функции g(x) показан на рис. 2. Данный график построен
в среде MathCAD.
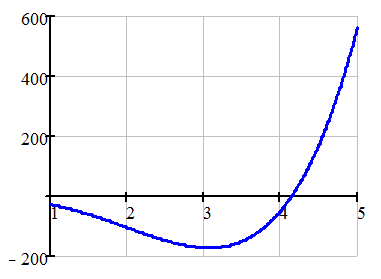
Рис. 2. График функции
g(x)
Из графика видно, что функция пересекает ось абсцисс на отрезке
[4,5]. Составим алгоритм нахождения корня
уравнения g(x) на этом отрезке. Блок-схема
алгоритма показана на рис. 3.
2.1.1. Блок-схема алгоритма
Рис. 3. Алгоритм решения
задачи
Описание алгоритма.
Блок-схема
алгоритма состоит из 9-ти блоков. После запуска
алгоритма в блоке 2 задаются начальное a и
конечное b значения отрезка, на котором
находится корень, а также точность e
его нахождения. Блоки 3 - 7 образуют цикл, при помощи которого производится
нахождение корня. Сначала в блоке 3 рассчитывается середина отрезка
x, затем вычисляется значение функции
f в этой точке. Далее в блоке 4 проверяется
условие f < 0, по которому
происходит ветвление алгоритма. Если условие выполняется, то в блоке 6 точка
a переносится в середину отрезка, иначе в
блоке 5 в середину отрезка переносится точка b.
Таким образом отбрасывается половина исходного отрезка и создается
новый отрезок вдвое меньшей длины. А блоке 7 производится проверка условия
сжат ли отрезок в длину, которая меньше заданной точности. Если условие не
выполняется, то управление передается на блок 3, где начинается новый виток
цикла сжатия отрезка, на котором находится корень уравнения g(x).
Циклический процесс повторения блоков 3 - 7 продолжается до тех пор, пока не
выполнится условие блока 7. По окончании цикла в блоке 8 выводится
найденный корень и в блоке 9 алгоритм заканчивает работу.
Создайте
блок-схему алгоритма при помощи программы Microsoft
Visio.
2.1.2. Приложение на
Delphi
Реализуем
составленный алгоритм в среде Delphi и
найдем корень упомянутого уравнения.
Запустим Delphi XE7 и создадим новое
приложение. Примеры создания приложения можно найти в методических указаниях
по лабораторным работам в среде Delphi по курсу
"Информатика".
Положите на
форму кнопку (компонент TButton), метку
(TLabel) и строку ввода (TEdit).
Вид формы показан на рис. 4.
Рис. 4. Окно приложения Delphi
С помощью
кнопки будем запускать алгоритм нахождения корня. Результат решения
уравнения будем выводить в строку ввода.
Щелкнув
дважды на кнопке, создадим для нее событие
OnClick и вставим в него код, который
показано на рис. 5.
procedure
TForm1.Button1Click(Sender: TObject);
var a,b,e,g,x: Double;
begin
a:= 4; b:= 5; e:= 0.001;
repeat
x:= (a+b)/2;
g:= 5*Power(x,4)-20*Power(x,3)-16*x+1;
if g < 0 then a:= x else b:= x;
until b-a < e;
edit1.text:= FloatToStr(x);
end;
Рис. 5. Код обработчика события
OnClick
Дадим
пояснение этому коду.
Ниже
заголовка процедуры объявлено 5 вспомогательных переменных a,b,e,g,x вещественного типа
Double.
Сам исполняемый код расположен между ключевыми словами
begin и end.
Сначала
вставим 3 оператора присваивания начальных значений переменным, которые
содержатся в блоке 2 алгоритма.
При помощи
цикла repeat until организуем процесс
поиска корня. Внутри цикла будем вычислять середину отрезка
x и значение функции g в этой
точке. Эти операторы содержатся в блоке 3
алгоритма. Для вычисления степени x будем
использовать функцию Power, описание которой
содержится в модуле math среды
Dephi. Чтобы функция была найдена приложением имя
этого модуля следует вставить в список используемых модулей
uses, который содержится в верхней части
секции interface модуля нашего
приложения.
Далее при
помощи условного оператора if проверим
выполнение условия блока 4 алгоритма и в зависимости от решения изменим
значение одного из концов отрезка a или
b. Циклический процесс нахождения корня
будем вести до выполнения условия, которое содержится в блоке 7.
По окончании
работы цикла с помощью функции FloatToStr
переведем найденный корень x из числового типа в
строковый и присвоим эту строку свойству Text
строки ввода Edit1.
Запустите приложение на выполнение и щелкните на кнопке
Button1. При этом выполнится процесс поиска
корня уравнения и результат будет отображен в компоненте
Edit1, как показано на рис. 6.
Рис. 6. Строка ввода Edit1 с найденным
корнем уравнения
Таким
образом, корень уравнения g(x) равен
x = 4,181 с точностью 0,001.
Сравните полученный результат с рисунком 2.
2.1.3. Сохранение программы и
уменьшение ее загрузочного модуля
Сохраните модуль Unit1 и сам проект в
отдельной папке. Для этого в Delphi
щелкните на кнопке SaveAll.
При этом откроется окно сохранения модуля Unit1.
Создайте в этом окне в удобном для Вас месте диска папку и сохраните
в ней этот модуль и проект под удобными для Вас именами (можно оставить те
имена, которые предлагает Delphi по
умолчанию).
Всегда
создавайте новую папку под каждый свой проект, разрабатываемый в
Delphi.
Запустите
программу на выполнение клавишей F9 или
кнопкой Run (кнопка с зеленым треугольником).
В результате Delphi создаст загрузочный
exe-модуль и запустит его на выполнение.
Закройте программу.
Найдем этот
модуль и определим его размер. Откройте Проводник, найдите папку с
проектом и откройте ее. Внутри папки появилась папка
Win32. Внутри этой папки находится папка
Debug (отладочные данные),
в которую Delphi поместила
exe-модуль. Это и есть готовая к использованию
программа, которую можно запускать на выполнение и без
Delphi. Если посмотреть свойства этого
файла, то можно убедиться, что его размер составляет примерно 11 Мб.
Это довольно большой размер. Однако есть возможность уменьшить его
примерно в 5 раз за счет удаления из файла отладочных данных.
Зайдите в Delphi,
откройте проект, если он закрыт, и обратите внимание на правую часть окна,
где расположена секция Project Manager. Раскройте
в нем список Build Configuration и обратите внимание, что жирным
помечен установленный отладочный режим Debug (рис. 7).
Наведите курсор мыши на режим Release, щелкните
правой клавишей на нем и выпавшем меню щелкните на команде Activate
(рис. 8). Теперь режим выполнения программы без средств отладки.
Снова
запустите программу, затем закройте ее. Теперь в папке
Win32. должна появиться папка Release,
в которой находится вновь скомпилированный exe-модуль.
Обратите внимание, что размер такого файла составляет примерно 2 Мб, что
в 5 раз меньше предыдущего варианта этого модуля. Папку Debug
можно удалить, чтоб она не занимала дисковое пространство памяти.
Рис. 7 |
|

Рис. 8 |
Есть и другие
способы дальнейшего уменьшения размеров exe-файла.
Например, к нему можно применить программу ASPack,
которая сожмет файл еще примерно в 3 раза, при этом его размер
составит примерно 0,6
Мб. Таким образом, применение этих двух методов позволяет уменьшить
размер исполняемого файла примерно в 20 раз.
2.2. Цикл с известным числом
повторов
Использование такого цикла
продемонстрируем на примере решения задачи численного интегрирования. Методы
численного интегрирования основаны на геометрическом представлении
определенного интеграла 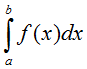 ,
значение которого равно площади криволинейной трапеции, ограниченной
графиком функции y = f(x), осью абсцисс и прямыми х = а, х
= b. ,
значение которого равно площади криволинейной трапеции, ограниченной
графиком функции y = f(x), осью абсцисс и прямыми х = а, х
= b.
Численные методы
являются приближенными, ибо площадь криволинейной трапеции заменяется суммой
площадей более простых фигур, например прямоугольников, как показано на рис.
9. Согласно этим методам отрезок интегрирования [а, b] разбивается на
n равных частей, образуя совокупность из
n отрезков одинаково малой
длины. Затем на каждом таком отрезке подынтегральная функция по
определенным соображениям заменяется отрезком прямой, используемой для
построения прямоугольника, и далее считают, что интеграл будет приближенно
равен сумме площадей прямоугольников, соответствующих упомянутым малым
отрезкам.
Рис. 9. К методу прямоугольников
Например, будем определять
горизонтальный отрезок по значению функции в левых точках каждого малого
отрезка. Тогда можно записать очевидную формулу вычисления интеграла
 . При этом значение функции в
текущей точке с номером i
можно найти по формуле . При этом значение функции в
текущей точке с номером i
можно найти по формуле 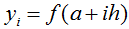 ,
где h = (b-a)/n
- шаг численного интегрирования. ,
где h = (b-a)/n
- шаг численного интегрирования.
2.2.1. Блок-схема алгоритма
Для
разработки блок-схем циклических алгоритмов нам потребуются
дополнительные элементы (блоки) начала и конца
цикла, которые представлены в таблице 1.
Таблица 1
|
Название |
Элемент (блок) |
Комментарий |
|
Границы цикла |
 |
Верхняя граница |
 |
Нижняя граница |
|
Нижняя граница цикла в
Visio получается поворотом блока верхней границы. При
этом, правда, переворачивается и текст внутри блока. Однако такой текст тоже
можно перевернуть.
Для примера вычислим
приближенно определенный интеграл
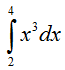 , разбив отрезок интегрирования
на 10 частей. , разбив отрезок интегрирования
на 10 частей.
Блок-схема
алгоритма вычисления интеграла представлена на рис. 10.
Рис. 10. Циклический алгоритм вычисления
определенного интеграла
Описание алгоритма.
Блок-схема
представленного на рис. 10 алгоритма приближенного вычисления определенного
интеграла состоит из 9-ти блоков. В блоке 2 заданы
пределы интегрирования a, b и число
n разбиений отрезка интегрирования. В блоке 3
производится вычисление шага интегрирования h
и обнуляется переменная s,
которая предназначена для суммирования площадей прямоугольников.
Теперь
следует найти сумму площадей прямоугольников. Поскольку у всех
прямоугольников ширина одинакова, то для ускорения работы алгоритма можно
сначала просуммировать лишь их высоты, а затем результат умножить на их
общую ширину h. Для суммирования
высот прямоугольников предназначен цикл
блоков 4 - 6. Счетчик цикла i на
каждом витке цикла последовательно принимает значения от 0 до
n-1. При этом к
переменной s добавляется высота
текущего прямоугольника. По окончании работы цикла переменная
s будет численно равна сумме
высот всех прямоугольников. Умножив в блоке 7 эту сумму на шаг
интегрирования h, получим
приближенное значение интеграла. В блоке 8 найденное значение
s выводится на
печать и в блоке
9 алгоритм заканчивает работу.
Создайте
блок-схему этого алгоритма при помощи программы Microsoft
Visio.
2.2.2. Приложение на
Delphi
Реализуем
составленный алгоритм в среде Delphi и
вычислим определенный интеграл по разработанной блок-схеме.
Создадим
новое приложение и положим на него компоненты, как показано на рис. 11.
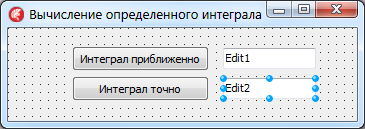
Рис. 11. Окно приложения для вычисления
определенного интеграла
Обработчик
события для щелчка на верхней кнопке показан ниже
procedure
TForm1.Button1Click(Sender: TObject);
var a,b,h,s: Double; n,i: Integer;
begin
a:= 2; b:= 4; n:= 10;
h:= (b-a)/n; s:= 0;
for
i:= 0 to n-1 do
s:= s+Power(a+i*h,3);
s:= s*h;
edit1.text:= FloatToStr(s);
end;
В данной
процедуре производится приближенное вычисление интеграла по алгоритму,
показанному на рис. 10. В процедуре использовано 4 вспомогательных переменных
a,b,h,s вещественного типа Double и две переменных n,i
целочисленного типа Integer. Исполнительная часть алгоритма состоит
из операторов, заключенных в наружные операторные скобки
begin end. Сначала следуют операторы присваивания начальных
значений, вычисления шага интегрирования h
и обнуления сумматора s.
Операторы
цикла выделены желтым цветом. Для создания цикла использована
его разновидность for do. Цикл
состоит из заголовка, в котором указаны пределы изменения счетчика
цикла i, и тела цикла, состоящего из
одного оператора, в котором и производится суммирование.
За
циклом расположен оператор окончательного вычисления значения интеграла
s и и вывода его в строку
Edit1.
Теперь запрограммируем событие от щелчка на кнопке с надписью
"Интеграл точно". Используемый нами интеграл допускает нахождение
его точного
значения по формуле Ньютона-Лейбница. Это значение равно
(44-24)/4.
Поэтому текст обработчика события для щелчка на данной кнопке может
выглядеть, например, так
procedure
TForm1.Button2Click(Sender: TObject);
begin
edit2.text:= FloatToStr((Power(4,4)-Power(2,4))/4.0);
end;
Результат работы программы показан
ниже на рис. 12.

Рис. 12. Результаты вычисления
определенного интеграла
Видно, что
приближенное значение интеграла заметно отличается от точного значения.
Поэтому на практике метод прямоугольников применяется редко.
2.3. Структуры вложенных циклов
Весьма часто при решении
алгоритмических задач приходится использовать конструкции, когда внутри
одного цикла может находиться один или несколько внутренних циклов. Такие
конструкции называются структурами вложенных циклов. Внутренние циклы должны
полностью входить в содержащие их наружные циклы.
Покажем
работу вложенных циклов на примере разработки алгоритма нахождения суммы
s = 11
+ 22 +...+ nn, где
n - некоторое целое положительное число. В наружном
цикле будем накапливать сумму, а во внутреннем - степень числа,
представляющего текущее слагаемое такой суммы.
2.3.1. Блок-схема алгоритма
Блок-схема
алгоритма показана на рис. 13.
Рис. 13. Алгоритм со структурой
вложенных циклов
Описание алгоритма.
Блок-схема
представленного на рис. 13 алгоритма состоит из 12-ти блоков. В блоке 2
выполняется ввод числа
n. В блоке 3 обнуляется переменная s,
которая предназначена для нахождения суммы.
Ниже в блоках
4 - 10 расположен цикл, на каждом витке в котором происходит нахождение
текущего слагаемого суммы и добавление его к значению переменной
s. Для этого в блоке 4, который
является заголовком цикла, его счетчик
i в процессе выполнения цикла последовательно принимает
значения от 1 до n по
количеству слагаемых.
В блоках 5 - 8
выполняется формирование слагаемого q,
соответствующего текущему значению переменой i.
В блоке 5 сначала переменной q
присваивается значение 1. Само слагаемое формируется во внутреннем по
отношению 4 - 10 цикле, образованном блоками 6 - 8. В это цикле будет
совершено i витков, на каждом из
которых счетчик цикла j будет
последовательно принимать значения 1, 2, ..., i.
При этом в теле внутреннего цикла, которое состоит из блока 7, будет
последовательно сформировано число q,
равное ii. В блоке 9 это
число будет добавлено к сумме s.
После выполнения
циклов в блоке 11 будет выведено значение переменной
s и в блоке 12 алгоритм закончит работу.
Создайте
блок-схему этого алгоритма при помощи программы Microsoft
Visio.
2.3.2. Приложение на
Delphi
Реализуем
составленный алгоритм в среде Delphi и
вычислим сумму по разработанной блок-схеме.
Создадим
новое приложение и положим на него компоненты, как показано на рис. 14.

Рис. 14. Форма приложения На форме находится 2 метки с
поясняющими надписями n: и
s:. Справа от первой из них лежит
компонент TSpinEdit, который в
Delphi находится на закладке
Samples. С помощью этого компонента можно задавать
целое число. Будем использовать его для задания значения переменной
n. Вычисленную сумму будем выводить
в компонент TEdit, который лежит
справа от метки с надписью s:. В
середину положите кнопку TButton и
двойным щелчком на ней создайте обработчик события
OnClick.
Полный текст
этой процедуры приведен ниже
procedure
TForm1.Button1Click(Sender: TObject);
var i,j,s,q: Integer;
begin
s:= 0;
for
i:= 1 to SpinEdit1.Value do
begin
q:= 1;
for j := 1 to
i do
q:= q*i;
s:= s+q;
end;
Edit1.Text:= IntToStr(s);
end;
В процедуре используется 4
вспомогательных переменных i,j,s,q
целочисленного типа
Integer.
Вычисления
производятся при помощи операторов, заключенных в наружные операторные
скобки begin end. В начале вычислений
переменная s предварительно
обнуляется. Далее следуют операторы наружного цикла, которые выделены желтым
цветом. В заголовке цикла for do переменная
i будет на каждом витке цикла
последовательно менять значение от 1 до
SpinEdit1.Value,
то есть до того значения переменной n,
которое определено пользователем в данном компоненте. В теле этого цикла,
которое состоит из операторов, расположенных между внутренними операторными
скобками begin end, производится
формирование отдельного слагаемого q,
соответствующего текущему значению переменной i.
Сначала ему присваивается значение 1. Затем во внутреннем цикле,
операторы которого выделены зеленым цветом, происходит перемножение числа
i само на себя i
раз, что равно текущему значению данного слагаемого. После цикла это
слагаемое добавляется к s.
Вычисленная
сумма выводится в компонент Edit1. Пример
вычислений для n = 4 показан
ниже на рис. 15.
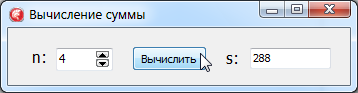
Рис. 15. Форма с вычисленной суммой
Проведите
вычисления для нескольких значений переменной n
и внесите их в Ваш отчет в
документе Word.
3.
Индивидуальные задания
Разработайте блок-схему алгоритма
и соответствующую программу на Delphi по своему индивидуальному варианту. Опишите
блок-схему своего алгоритма и
код программы.
Варианты
индивидуальных заданий приведены в таблице 2.
Таблица 2
| №1 |
Модифицируйте метод вычисления
определенного интеграла на случай
определения высоты прямоугольников по правым концам отрезков |
№2 |
Модифицируйте алгоритм
вычисления определенного интеграла так, чтобы его можно было
вычислять при значениях пределов интегрирования
a и
b, которые вводит пользователь
программы |
| №3 |
Найти сумму 1+2m+3m+...+nm,
где n, m - целые
положительные числа |
№4 |
Найти факториал целого числа
n! |
| №5 |
Найти такое число k, при
котором сумма 1+3+5+...+ k
впервые превысит некоторое число
n |
№6 |
Модифицируйте алгоритм вычисления
определенного интеграла так, чтобы его можно было вычислять при
любом заданном числе разбиений отрезка интегрирования |
| №7 |
Составите алгоритм вычисления
определенного интеграла для функции ln(sin(3+x)+cos(3+x)
+3)
на произвольном отрезе [a,
b] при количестве разбиений этого отрезка
n = 20 |
№8 |
Найти сумму 1+1/22+33+1/44+55+...+nn,
где n - нечетное число |
| №9 |
Задатся три
произвольных числа. Найти среди них наименьшее
и наибольшее числа |
№10 |
Модифицируйте метод вычисления
определенного интеграла на
случай определения высоты прямоугольников по серединам отрезков |
|