Алгоритмы обработки данных
Коднянко В.А.
Лабораторный
практикум
Тема № 4
В спомогательные алгоритмы-функции
Как отмечалось в предыдущем разделе, вспомогательный алгоритм-функция похож
на алгоритм-процедуру, однако есть и различия - имя функции выступает также в роли
переменной, куда записывается результат
работы этого вспомогательного алгоритма.
4.1.
Алгоритмы-функции
Рассмотрим задачу о вычислении значения функции ошибок (другие
названия - функция Лапласа, интеграл вероятности), которая находит широкое
использование в теории вероятностей, статистике и теории дифференциальных
уравнений в частных производных. Она определяется как
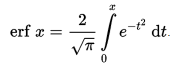
Данный интеграл нельзя вычислить
точными методами, поэтому найдем интеграл приближенно по формуле Симпсона.
Формула получила название в честь британского математика Томаса Симпсона
(1710—1761).
Согласно
методу отрезок интегрирования [a, b]
разбивают на четное число n частей
одинаковой длины h = (b-a)/n, как показано
на рис. 1.
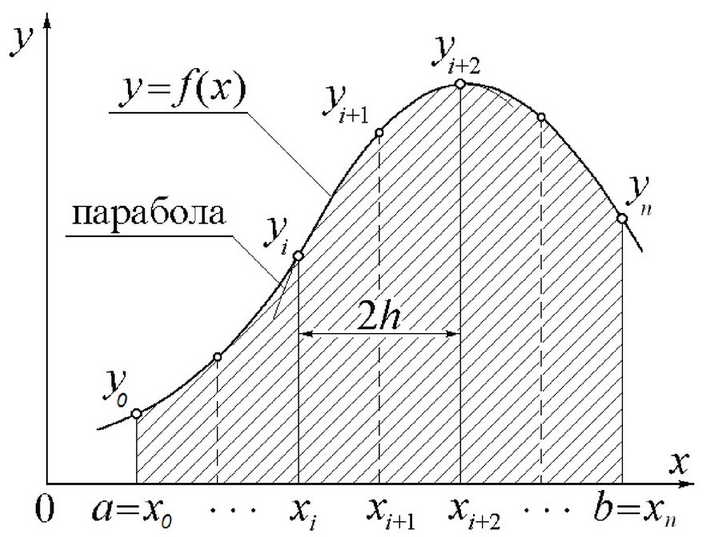
Рис. 1. К формуле Симпсона
Далее в
точках x0, x1,
..., xn вычисляют значения
подынтегральной функции yi
= f(xi), i = 0,1,..., n
и находят интеграл по формуле
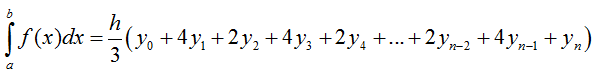
Суть метода состоит в том, что через
каждые 3 соседних точки на кривой проводят параболу и затем находят площади
фигур с помощью точной формулы. Сложив эти площади, получают приближенное
значение интеграла. Формула Симпсона имеет высокую степень точности, поэтому
на практике она находит широкое применение.
Для решения
задачи составим 3 вспомогательных алгоритма-функции. Первый предназначен
для вычисления значения подынтегральной функции, второй - для вычисления
интеграла по формуле Симпсона и третий для вычисления функции ошибок.
Первый
алгоритм показан на рис. 2.
Рис. 2. Блок-схема алгоритма вычисления
значения
подынтегральной функции f(x)
Обратите внимание, что алгоритм
содержит оператор, в котором явно присвоено значение имени функции, в данном
случае это f.
Теперь составим блок-схему
алгоритм-функции вычисления интеграла по формуле Симпсона. Она приведена на
рис. 3.
Рис. 3. Блок-схема алгоритма вычисления
определенного интеграла по формуле Симпсона
Функция имеет имя Simps и четыре параметра
- пределы интегрирования a, b, число
разбиений n отрезка интегрирования и имя
подынтегральной функции f.
В блоке
2 вычисляется шаг интегрирования
h и определяется значение переменной
k = 4. В
блоке 3 вычисляется сумма значений функции f
на концах отрезка, что соответствует сумме y0
+ yn. В цикле блоков 4 - 6 к
этой сумме добавится оставшаяся часть суммы, расположенной в круглых скобках
формулы Симпсона. На выходе из цикла определится окончательное значение
интеграла.
Алгоритм
вычисления функции ошибок определим через функцию
Simps, как показано на рис. 4.
Рис. 4. Блок-схема алгоритма
вычисления функции ошибок Erf(x)
Значение алгоритм-функции ошибок
Erf зависит от от аргумента
x, числа n
разбиений отрезка интегрирования и подынтегральной функции
f.
Осталось
только составить головной алгоритм. Он показан на рис. 5.
Рис. 5. Головной алгоритм
вычисления функции ошибок Erf
Создайте
блок-схемы алгоритмов при помощи программы Microsoft
Visio.
Реализуем
вспомогательный и головной алгоритмы в среде Delphi.
Запустим Delphi XE7 и создадим новое
приложение.
Положите на
форму три метки TLabel,
два компонента TSpinEdit, один
компонент TEdit,
компонент TStringGrid
и кнопу TButton,
как показано на рис. 6. На
метках должны быть надписи
n, x, m. Первый
TSpinEdit должен иметь имя seN,
второй - seM. Строке
TEdit дайте имя eX,
а сетке - Sg.
С помощью
первого TSpinEdit будем задавать число
разбиений n, с помощью второго - номер
m строки в сетке, в которую будет выводить
результаты. TEdit потребуется для ввода
значения аргумента. Кнопкой будем запускать
вычисление интеграла.
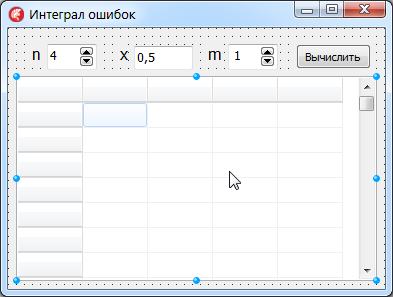
Рис. 6. Окно приложения Delphi
Перейдите в редактор кодов и введите описание типа
TFun и функции
f, как показано на рис. 7.
Тип TFun описывает функцию типа
Double с единственным аргументом того же
типа. Ниже расположено описание функции
f, которое начинается ключевым словом
function. В теле функции
находится единственный оператор вычисления значения функции
f через аргумент
x. Обратите внимание, что
значение функции присваивается переменной
Result.
Текст процедуры Perm
открывается ключевым словом procedure. Далее
расположено имя процедуры и в скобках указаны формальные параметры
a
и b. Эти параметры
являются переменными, так как перед ними расположен описатель
var. Переменные имеют тип Double -
то есть вещественный тип. После заголовка процедуры
объявлена вспомогательная переменная c,
которая имеет тот же тип. Далее в теле процедуры, которое
находите внутри блоков begin end, расположены
операторы перестановки значений переменных. Текст процедуры вспомогательного
алгоритма готов.

Рис. 7.
Код типа функции и функции f
Ниже этих операторов
добавьте код функции Simps, который
приведен на рис. 7. Данная функция содержит 4 параметра - пределы
интегрирования a, b,
число разбиений n и имя
интегрируемой функции f, каждый из которых
имеет свой тип. Ниже объявлено несколько вспомогательных переменных.
В теле
функции сначала вычисляется сумма s
значений функции на краях отрезка интегрирования, определяется переменная
k и шаг интегрирования
h. Затем фв цикле накапливается оставшаяся
часть суммы формулы Симпсона. В заключение переменной
Result присваивается значение равное вычисленному интегралу.

Рис. 8.
Код функции Simps
Вслед
за этими операторами поместите текст функции
Erf, как показано на рис. 9.

Рис. 9.
Код функции Erf
Теперь все
вспомогательные функции запрограммированы и осталось лишь создать обработчик события
от щелчка на кнопке и наполнить эту процедуру операторами вычисления
интеграла. Текст этой процедуры показан на рис. 10.

Рис. 10.
Код обработчика события OnClick
для кнопки
В теле этой процедуры сначала в переменные n
и m
переносятся значения
соответствующих компонентов типа TSpinEdit.
Напомним, что первый из этих параметров определяет на
сколько частей следует делить отрезок интегрирования
[0, x] при вычисления
интеграла по формуле Симпсона. Второй играет вспомогательную роль, он будет
указывать номер строки сетки, в которую следует выводить результат. Параметр
x определяет значение
аргумента, которое будем набирать в строке eX.
Далее следует
несколько операторов, которые предназначены для вывода надписей. Например,
оператор Sg.Cells[2,0]:= 'x' выведет надпись 'x' в клетку
сетки, которая находится на пересечении второго столбца и нулевой строки
(см. рис. 11).
Оператор
Sg.Cells[0,m]:= IntToStr(m) выведет номер строки m
в клетку, которая находится на пересечении нулевого столбца и строки
с номером m. Оператор
Sg.Cells[2,m]:= eX.Text выведет вы сетку аргумент, а оператор Sg.Cells[3,m]:=
FloatToStr(Erf(x,n,f)) вычислит интеграл по формуле Симпсона и затем
выведет его в сетку.
Примеры
вычислений интеграла ошибок для x = 1,5 и
разных значений параметра n показаны на
рис. 11.
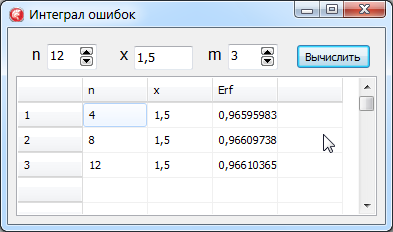
Рис. 11.
Окно вычислений интеграла ошибок
Анализ метода показывает, что чем больше число
n частей разбиений отрезка интегрирования, тем
точнее будет вычислен определенный интеграл. Однако слишком большое
n может замедлить метод, а при малом
n точность вычислений может
оказаться недостаточной. Считается более правильным подход, когда при
вычислении интеграла задаются точностью расчета, на основе которой
определяют требуемое число n. Такой
подход называется методом Симпсона с автоматическим выбором шага.
Суть метода
такова. В качестве параметра, определяющего точность формулы, задают малую
величину e, которая определяет максимальное
отклонение приближенного значения интеграла от его точного значения.
Далее вычисляют интеграл по формуле
Симпсона при n = 4 и при
n = 8. Если абсолютная величина разности интегралов меньше
e, то считается что интеграл вычислен. Если
же условие не выполняется, то вычисляют интеграл при n
= 16 и сравнивают его с предыдущим значением интеграла. Процесс
удвоения числа разбиений ведется до тех пор, пока не выполнится упомянутое
условие.
Блок-схема
алгоритма вычисления интеграла по формуле Симпсона с автоматическим выбором
шага показана на рис. 12.
Рис. 12. Алгоритм
вычисления определенного интеграла
по формуле Симпсона с автоматическим выбором шага
В блоке 2
сначала вычисляется интеграл s1 при
n=4 и в блоке 3 задается
n=8. Далее процесс вычислений производится
в цикле, образованном блоками 4-6. В блоке 4 вычисляется
s2, как интеграл с удвоенным числом разбиений и проверяется условие
блока 5 о сходимости к результату. Если оно не выполняется, то в блоке 6
последнее значение интеграла записывается в s1,
число разбиений удваивается и в блоке 4 вычисляется новый интеграл. Цикл
выполняется до тех пор, пока не выполнится условие 5.
Аналогичные изменения придется внести и алгоритм вычисления интеграла
ошибок. Новая функция ErfA будет выглядеть
так, как показано на рис. 13.
Рис. 13. Блок-схема алгоритма
вычисления функции ошибок ErfA(x) Внесем изменения
в программу. Добавите на форму дополнительные компоненты с тем, чтобы можно
было провести вычисления по алгоритму с автоматическим выбором шага. Эти
компоненты показаны на рис. 14.
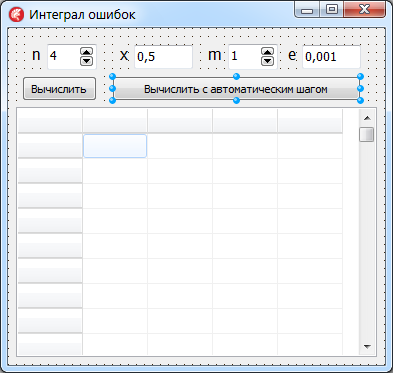
Рис. 14. На форму добавлено 3 новых
компонента для обеспечения
вычислений с автоматическим выбором шага
Перейдите в редактор кода и
добавьте текст двух новых функций, как показано на рис. 15.

Рис. 15. Функции
SimpsA и ErfA
Осталось только создать обработчик события для щелчка на кнопке с надписью "Вычислить
с автоматическим шагом". Текст обработчика показан на рис. 16.

Рис. 16.
Код обработчика события OnClick
для кнопки
с надписью "Вычислить с автоматическим шагом"
Пример выполнения программы для новой функции показан на рис. 17.
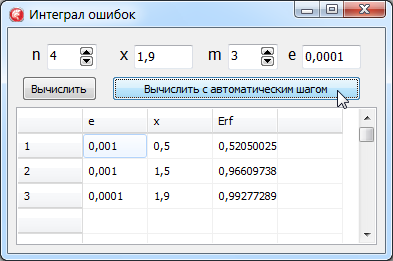
Рис. 17. Вычисление функции ошибок по
формуле Симпсона
с автоматическим выбором шага
4.2. Индивидуальные задания
Разработайте блок-схемы алгоритмов-функций,
а при необходимости и алгоритмов-процедур, головного алгоритма
и соответствующую программу на Delphi по своему индивидуальному варианту. Опишите
блок-схемы алгоритмов и
код программы.
Варианты
индивидуальных заданий приведены в таблице 1.
Таблица 1
| №1 |
Дано два произвольных одномерных массива
одинаковой длины. Сформируйте третий массив, как сумму первых
двух массивов. |
№2 |
Подсчитайте количество
одинаковых пар соседних элементов в трех одномерных массивах произвольной длины |
| №3 |
Вычислите определенный
интеграл методом прямоугольников с автоматическим выбором шага |
№4 |
Дано 2 произвольных одномерных массива.
Найдите количество положительных элементов в этих массивах |
| №5 |
Есть 3 произвольных одномерных массива.
Укажите номер массива, сумма элементов в котором наибольшая |
№6 |
Есть 2 произвольных одномерных массива
одинаковой длины.
Установите равны ли эти массивы |
| №7 |
Есть 2 произвольных
одномерных массива. Который из массивов имеет больше
положительных элементов? |
№8 |
Дано 3 одномерных массивах одинаковой длины.
Найдите общую сумму их отрицательных элементов |
| №9 |
Есть 3 произвольных одномерных массива.
Сформируйте 4-й массив из 3-х элементов, где 1-й элемент будет
равен сумме положительных элементов 1-го массива, 2-й - 2-го,
3-й - 3-го. |
№10 |
Подсчитайте количество
элементов в трех одномерных массивах произвольной длины, которые
равны некоторому числу |
|